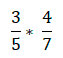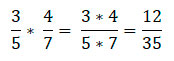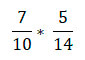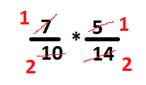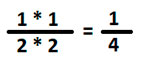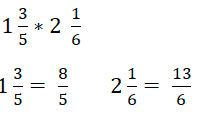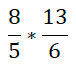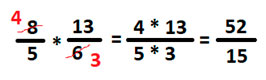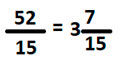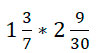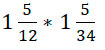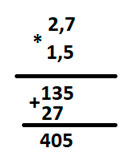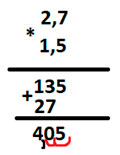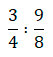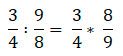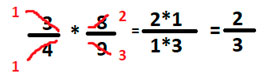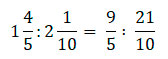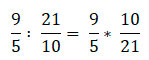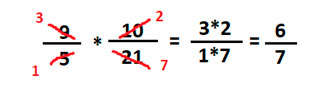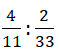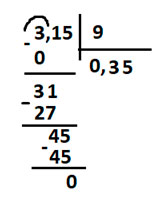Необходимым навыком для каждого ученика пятого класса является умение выполнять умножение и деление дробей.
Разберём каждую тему подробнее.
Умножение обыкновенных дробей
Рассмотрим две обыкновенные дроби и выполним их умножение:
Сначала смотрим, можно ли сократить числители дробей со знаменателями. В нашем случае 3 и 4 не имеют общих делителей и с числами 5 и 7, поэтому сократить дроби невозможно.
Значит, начинаем умножать в лоб, числитель на числитель, знаменатель на знаменатель
Числитель меньше знаменателя, а значит, целую часть выделить невозможно,
Это окончательный ответ.
Разберём еще один пример:
В этой ситуации можно сократить числа 7 и 14, 10 и 5. Поэтому в первую очередь сокращаем дроби, чтобы упростить будущие вычисления
В итоге мы получили:
Задание для самопроверки:
Умножение смешанных дробей
Согласно правилам, умножение смешанных дробей выполнить невозможно, поэтому в первую очередь переводим каждую смешанную дробь и неправильную.
*см. перевод смешанной дроби в неправильную
Рассмотрим пример,
Мы получили:
Выполняем сокращение дробей, а затем умножаем их
Так как 52 > 15, выделяем целую часть
Задание выполнено
Задание для самопроверки:
Умножение десятичных дробей
Выполним умножение десятичных дробей: 2,7 * 1,5.
Для этого умножим данные числа «столбиком», не обращая внимания на запятую.
При умножении, количество знаков после запятой складывается. У первого и у второго числа по одной цифре после запятой, значит при их умножении у числа будет уже 2 знака после запятой, так как 1+1 = 2
Ставим запятую в нужное место
Мы получили, что 2,7 * 1,5 = 4,05
Задание для самопроверки:
- 8,7 : 0,3
- 1,24 : 3,1
- 51,2: 0,64
Деление обыкновенных дробей
При делении обыкновенных дробей действуем следующим образом, деление заменяем на умножение, при этом переворачиваем вторую дробь.
Умножаем дроби по правилам умножения обыкновенных дробей.
Сокращаем числитель со знаменателем, 3 и 9 сокращаются на 3, а 4 и 8 на 4 соответственно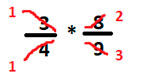
Умножаем верх на верх, а низ на низ у каждой дроби
Умножение выполнено.
Деление смешанных дробей
Ни умножение, ни деление смешанных дробей выполнить невозможно, поэтому переводим смешанную дробь в неправильную.
А затем выполняем замену деления на умножение, переворачивая вторую дробь
Сокращаем числитель со знаменателем, а зачем умножаем дроби, верх на верх, низ на низ соответственно
Задание для самопроверки:
Деление десятичных дробей
- Рассмотрим деление десятичных дробей на примере чисел 2,6 : 0,2
По правилу, делить на дробь нельзя, поэтому переносим запятую у делителя в конец числа, то есть на один знак вправо, при этом у делимого она также перенесется на знак в правую сторону.
И делим целые числа, будто запятой и не было вовсе.
Ответ готов, это число 13.
- Разделим 25,6 на 0,04
У делителя 2 знака после запятой, поэтому переносим ей вправо на 2 знака и у делимого и у делителя. Но, так как у делимого был всего 1 число после «,» , а нам необходим перенос на 2 знака, в конец этого числа припишем недостающее число 0. В нашем случае ровно один.
- Попробуем решить следующий пример с делением десятичных дробей: 0,315 : 0,9
У делителя 1 цифра после запятой, переносим её ровно на один знак у делимого и у делителя, получаем:
В этом случае сначала делим целую часть у делимого, то есть 3 на делитель, т. е. на 9. Но 3 < 9, поэтому берём по 0. После 0 в значении частного ставим запятую, списываем 1 и делим уже 31 на 9. Подбираем такое число, которое при умножении на 9 даёт число, близкое к 31, но чуть меньше, 9 * 3 = 27, берём по 3. 31-27 = 4, списываем 5, делим уже 45 на 9, получаем 5
В итоге наш ответ – 0,35.