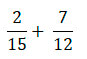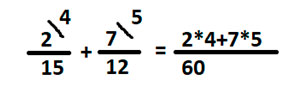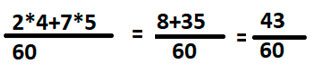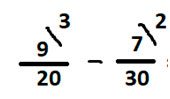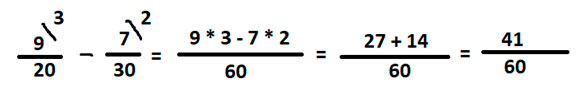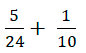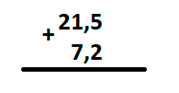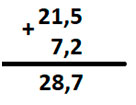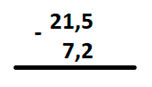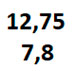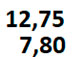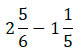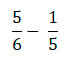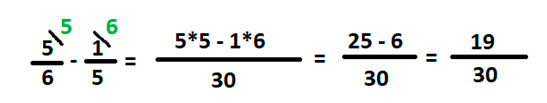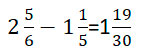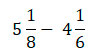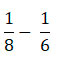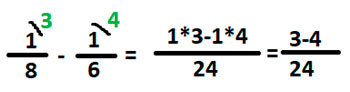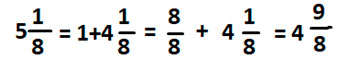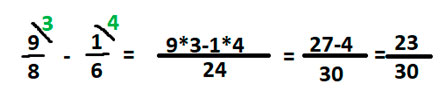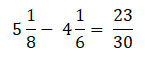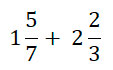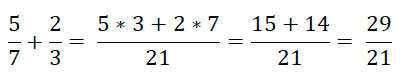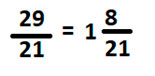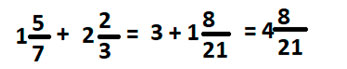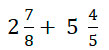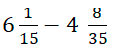Рассмотрим непростую, но очень важную тему 5 класса по математике «сложение и вычитание дробей». Мы научимся складывать дроби как с общим, так и с разными знаменателями, разберёмся со смешанными дробями, научимся выполнять арифметические действия и с десятичными дробями.
Сложение и вычитание дробей с общим знаменателем
Допустим, по условию задания нам нужно найти сумму:
Так как в этом примере знаменатель у чисел одинаковый, это число 5, мы можем записать их под общую черту
Выполняем сложение числителей 2 и 1, 2 + 1 = 3
Тем самым получили
Найдем разность
Знаменатель у дробей общий, записываем их под одну черту и выполняем вычитание числителей 11 – 3 = 8
Получили
Тем самым вы выполнили вычитание двух дробей с общим знаменателем.
Задание для самопроверки:
Вычислите:
Сложение и вычитание дробей с разными знаменателями
Для выполнения сложения или вычитания дробей с разными знаменателями, необходимо в первую очередь найти наименьшее общее кратное (НОК) имеющихся знаменателей. НОК и есть общий знаменатель для дробей. Для этого вспомним, данную тему:
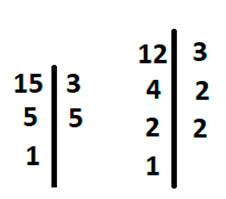
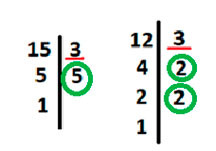
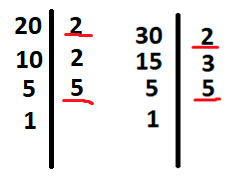
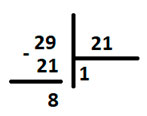
Найдем НОК (15,12). Для этого разложим каждое число на простые множители так, чтобы в конце получилась 1.
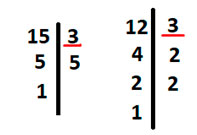
Подчеркнём одинаковые цифры во вторых столбцах у каждого числа.
Теперь возьмем первое число, то есть 15, и умножим его на неподчеркнутые цифры у второго числа. То есть 15 * 2 * 2, получим 60.
- Итак, теперь попробуем выполнить сложение дробей с разными знаменателями:
В первую очередь, найдем НОК знаменателей, 12 и 15.
Мы уже нашли его в предыдущем действии, НОК(12, 15) = 60
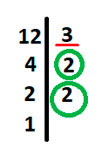
Теперь смотрим, на что нужно домножить первую дробь, чтобы ее знаменатель из 12 превратился в 60. Для этого вернемся к нахождению НОК и найдем неподчёркнутые цифры из другого столбца( смотрим на разложение числа 15), это число всего одно, 5. Мы поняли, что дополнительный множитель у первой дроби – это число 5.
Аналогично найдём дополнительный множитель для второй дроби, у второго числа 12 2 и 2 не подчёркнуты. 2*2 = 4 Следовательно дополнительный множитель для неё – это число 4.
Получившиеся доп. множители записываем соответственно в правом верхнем углу у каждой дроби. А затем умножаем числитель дробей на этот множитель, записываем получившееся выражение уже сверху дробной функции со знаменателем 60.
Выполним необходимые действия.
В итоге мы получили дробь, которая равна сумме двух первоначальных.
- Посмотрим, как выполнять вычитание дробей с разными знаменателями, например,
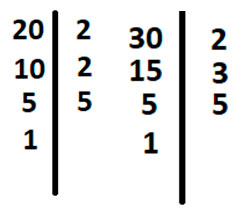
Также первоначально найдем НОК, разложим знаменатели дробей 20 и 30 на простые множители.
Подчеркнём одинаковые цифры в двух столбцах
Домножим 20 на неподчёркнутые цифры у 30, это лишь 3.
20 * 3 =60
НОК (20,30) = 60
Значит общий знаменатель искомых дробей – 60.
Посмотрим, какой недостающий множитель у числа 20, это цифра 3 из второго столбца.
А доп. множитель у 30 – цифра 2 из первого столбика.
Записываем дроби под общий знаменатель, при этом не забываем умножать числители на соответственный доп. множитель.
Это окончательный ответ.
Задание для самопроверки:
Сложение и вычитание десятичных дробей
Для того, чтобы научиться складывать и вычитать десятичные дроби, мы должны в первую очередь правильно их записать, запятая у второго числа должна находиться строго под запятой у первого.
Cложение десятичных дробей
Для этого суммируем цифры, находящиеся друг под другом, начиная с крайней левой. Записываем получившиеся значения под вертикальную черту. Если под одной из цифр нижняя отсутствует, как у числа 2, просто списываем эту двойку вниз.
5+2=7
1+7 = 8
Пишем ответ, оставляя запятую на прежней позиции.
Вычитание десятичных дробей
Это делается абсолютно аналогично сложению. Запишем числа друг под другом, запятая под запятой.
Начнём отнимать их верхнего числа нижнее.
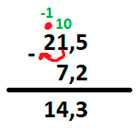
5-2 = 3
1-7 невозможно вычесть, так как 1<7, поэтому занимает у предыдущей цифры 1 десяток,
1+10=11
И уже 11-7 = 4
Переходим к крайней левой цифре, так как мы у нее занимали десяток, это число ученьшилось на 1, то есть 2-1=1
Первая цифра стала равна 1
В итоге мы получили:
Не забудьте про запятую!
Cложение десятичных дробей с разным количеством знаков после запятой
Расположим числа друг под дружкой так, чтобы запятая одной дроби находилась под запятой другой.
Выполним сложение, не обращая внимания на запятую.
12,75 + 7,8 = 20,55
- Рассмотрим вычитание десятичных дробей с разным количеством знаков после запятой
Снова располагаем числа друг под дружкой «запятая под запятой».
Допишем в конец второго числа нужное количество 0, так, чтобы у обоих слагаемых было одинаковое количество цифр после запятой. В нашем случае необходимо дописать всего один ноль
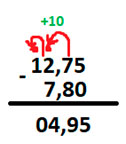
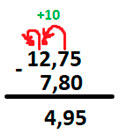
Вычтем из первого числа второе, запятую оставим на прежней позиции.
С 0 число начинаться не может, поэтому просто вычеркнем его.
Мы получили
Задание для самопроверки:
- 2,56 + 7, 62
- 11,7 – 3,28
- 1,11 – 1,6
Вычитание смешанных дробей
Изучим вычитание смешанных дробей на примере:
Для начала попробуем вычесть дробные части у данных чисел
Приведем к общему знаменателю, найдя НОК (5,6)
НОК (5,6) = 5*6 = 30
Следовательно, первую дробь домножаем на 5, вторую на 6 и считаем.
Теперь вычитаем целые части
2-1=1
Но не всегда возможно вычесть из первой дроби вторую, например,
Пробуем выполнить вычитание дробных функций
НОК(8, 6) = 24
*Нахождение НОК чисел в предыдущее теме
Просчитать значение числителя невозможно, так как 3 < 4
Поэтому занимаем 1 у целой части первой дроби и приводим эту единицу к знаменателю 8
И снова пробуем вычитать дробные части
Теперь вычтем целые части
4 – 4 = 0
То есть целой части нет
Следовательно,
Сложение смешанных дробей
Сложение смешанных дробей выполняется аналогично вычитанию.
Для этого сначала найдем сумму дробных частей. Рассмотрим пример:
Так как числитель больше знаменателя выделим целую часть:
*см. «выделение целой части»
Теперь сложим целые части:
1 + 2 = 3
Мы получили
Задание для самопроверки:

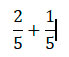
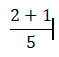
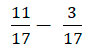
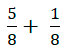 ;
;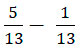 ;
;