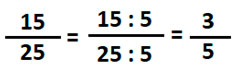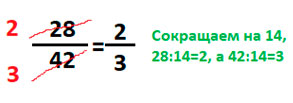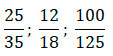Сокращение дробей – это и есть частное от деления верха (числителя) и низа (знаменателя) на их наибольший общий делитель, то есть на НОД, который мы уже научились находить в прошлой теме. То есть, по сути мы используем основное свойство дроби, которое разобрали в предыдущей теме.
При выполнении умножения и деления дробных чисел всегда рекомендуется сначала сократить дроби, если это возможно, а затем уже выполнять соответственно их умножение или деление.
Приведем пример, сократим 
. На какое число делится и 15 и 25 одновременно? Нетрудно догадаться, что это цифра 5. Начинаем делить и верхнюю и нижнюю часть дроби на 5.
После выполнения деления мы получили 
.
Для того, чтобы сэкономить время на контрольной или самостоятельной работе, при сокращении дробей можно выполнять сокращение сразу, зачёркивая начальные значения, написав рядом с ними уже получившиеся при делении, более маленькие числа.
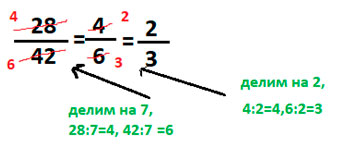
Не обязательно сразу сокращать дробь на большое число, нет ничего страшного в том, чтобы делать это постепенно, например:
После упрощения дроби мы получили 
.
Задание для самопроверки:
Сократите дробь:
