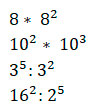Все мы знаем, что недостаточно научиться только лишь возводить число в степень, необходимо также понять и запомнить свойства степеней. Их равно 3. Но эти правила работают только, если основания, то есть числа, которые умножаются сами на себя, одинаковые. Если же у числа не было никакой степени, то принимаем её за 1.
Свойства степенных выражений:
- Если степенные функции с равными основаниями умножаются, то степени складываются, а основание остаётся прежним
Например,
![]()
![]()
- Если же они делятся, то соответственно показатели степени мы должны вычесть.
Посчитаем, чему равно значение выражения
![]()
![]()
- Если же у числа сразу несколько степеней, так называемое возведение «степень в степень», то они умножаются между собой
Допустим, ![]()
Разберём более трудные задания: ![]()
У первого числа основание 2, а второго – 8. А пока они разные, мы не имеем права выполнять действия. Поэтому сначала сведем их к общему меньшему основанию, то есть к 2.
![]()
Мы получаем,
![]()
Задание для самопроверки:
Вычислите: