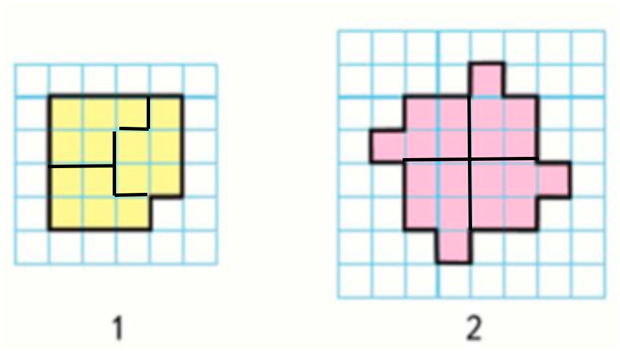
Номер 1
Начерти такие фигуры в тетради.
1) Раздели фигуру 1 на три равные части так, чтобы линии деления шли по сторонам клеток.
2) Раздели фигуру 2 на четыре такие же части, как в предыдущем задании. Линии деления также должны идти по сторонам клеток.
Номер 2
Три друга: Кирилл, Алексей и Глеб – участвовали в теннисном турнире. Один из этих мальчиков стал победителем турнира. На вопрос «Кто победил?» – Кирилл ответил: «Это не я». Алексей сказал: «Победителем стал Глеб». Позже выяснилось, что один из этих ответов верный, а другой нет. Кто победил в теннисном турнире?
Начни рассуждать так: «Предположим, что Алексей сказал правду, тогда и Кирилл …»
Предположим, что Алексей сказал правду, тогда и Кирилл сказал не правду, и победитель он, что невозможно. Следовательно Кирилл сказал правду, а Алексей – не правду, а значит победитель Алексей.
Номер 3
Мальчик купил несколько булочек по 17 р. Он подал на кассу 100 р. и получил сдачу в виде нескольких пятирублевых монет. Сколько пятирублевых монет он мог получить?
Если мальчик получил сдачу только пятирублёвыми монетами, то значит сумма покупки оканчивается на 5, следовательно мальчик мог купить только 5 булочек, и он потратил 17 ∙ 5 = 85 р., сдача составила 100 − 85 = 15 р., а количество пятирублёвых монет равно 15 : 5 = 3.
Номер 4
Используя в каждом случае 4 раза цифру 7, знаки арифметических действий и, если надо, скобки, составь 5 выражений со значениями: 5, 6, 7, 8, 9.
Например: 7 − (7 + 7) : 7 = 5
- 7 − (7 + 7) : 7 = 5
- (7 ∙ 7 − 7) : 7 = 6
- (7 − 7) ∙ 7 + 7 = 7
- (7 ∙ 7 + 7) : 7 = 8
- (7 + 7) : 7 + 7 = 9
