3. Среднее арифметическое двух чисел равно 72. Одно из чисел равно 95. Найди другое число.
Так как среднее арифметическое двух чисел на числовом луче находится по середине между данными числами, то:
72 − (95 − 72) = 72 − 23 = 49 − второе число.
Проверка:
(95 + 49) : 2 = 144 : 2 = 79 − среднее арифметическое.
Ответ: 49 − второе число.
4. В первый день туристы прошли 26 км, во второй − 35 км, в третий − 33 км, а в четвертый − 30 км. Сколько в среднем километров проходили туристы за один день?
(26 + 35 + 33 + 30) : 4 = 31 (км)
Ответ: 31 км в среднем километров проходили туристы за один день.
5. 1) Сколько квадратных дециметров в 1 (м2)?
2) Вырази в квадратных дециметрах: 3 (м2); 6 (м2); 8 (м2); 10 (м2).
1) 1 (м2) = 100 (дм2)
2) 3 * 100 = 300
3 (м2) = 300 (дм2)
6 * 100 = 600
6 (м2) = 600 (дм2)
8 * 100 = 800
8 (м2) = 800 (дм2)
10 * 100 = 1000
10 (м2) = 1000 (дм2)
6. Выполни действия.
(68 + 49) * 4 − 117 * 5 : 9 =403
1) 68 + 49 = 117
2) 117 * 4 = 468
3) 117 * 5 = 585
4) 585 : 9 = 65
5) 468 — 65 = 403
(187 + 369) : 4 + 124 * 6 : 8 = 232
1) 187 + 369 = 556
2) 556 : 4 =139
3) 124 * 6 =774
4) 774 : 8 = 93
5) 139 + 93 = 232
(76 + 58) * 3 + (218 + 247) : 5 = 495
1) 76 + 58 = 134
2) 218 + 247 = 465
3) 134 * 3 = 402
4) 465 : 5 = 93
5) 402 + 93 = 495
(389 + 276) : 7 − 135 * 4 : 6 = 5
1) 389 + 276 = 665
2) 665 : 7 = 95
3) 135 * 4 = 540
4) 540 : 6 = 90
5) 95 — 90 = 5
7. В пассажирском поезде 5 купейных и 9 плацкартных вагонов. В каждом купейном вагоне в среднем едет по 36 пассажиров, а в каждом плацкартном в среднем по 54 пассажира. Сколько всего пассажиров едет в этом поезде?
1) 5 * 36 = 180 (п.) в купейных вагонах
2) 9 * 54 = 486 (п.) в плацкартных вагонах
3) Найдем, сколько всего пассажиров в этом поезде:
180 + 486 = 666 (п.) всего в этом поезде
Ответ: 666 пассажиров.
8. Начерти в тетради отрезок AB длиной 8 см. Отметь на нем точку O так, чтобы длины отрезков AO и OB были равны. Построй окружность с центром в точке O и диаметром, равным длине
отрезка AB.
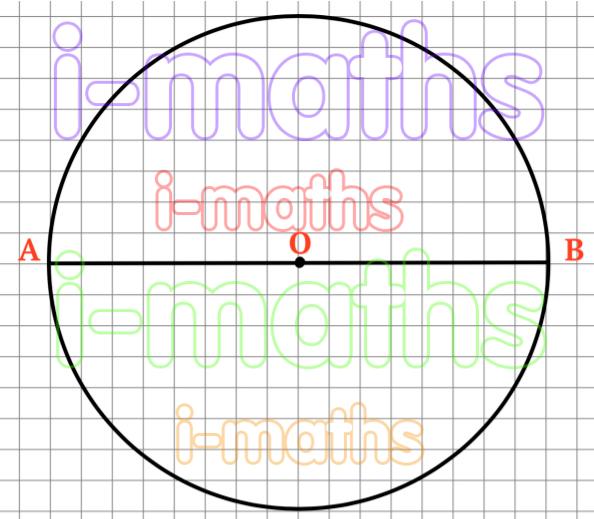
Нарисуем отрезок и отметим на нем точку O.
AB = 8 см, AO = OB = 4 см.
Построим окружность.
9. Имеются трехлитровая банка сока и две пустые банки: одна − литровая, другая − двухлитровая. Как разлить сок так, чтобы во всех трех банках было по одному литру?
Попробуй найти два способа решения.
1 способ:
1) Из трехлитровой банки наполнить литровую банку;
2) Перелить из литровой банки сок в двухлитровую;
3) Из трехлитровой банки наполнить литровую банку.
Ответ: в каждой банке будет по 1 литру сока.
2 способ:
1) Из трехлитровой банки наполнить двухлитровую банку;
2) Из двухлитровой банки наполнить литровую банку.
Ответ: в каждой банке будет по 1 литру сока.


