1. Рассмотри выражения в каждой рамке. Объясни порядок выполнения действий, указанный синими цифрами. Выполни вычисления. Сравни значения выражений.

2. Укажи порядок выполнения действий и вычисли значения выражений. Сравни выражения и их значения. Сделай вывод.

Ответы разные, значит порядок действий имеет большое значение.
3. Садоводам надо было посадить 230 кустов смородины и 150 кустов крыжовника. В первый день они посадили 8 рядов смородины, по 20 кустов в каждом ряду, и 4 ряда крыжовника, по 30 кустов в каждом ряду. Объясни, что означают выражения.
230 + 150 − кустов смородины и крыжовника надо посадить
садоводам;
150 − 30 * 4 − крыжовника осталось посадить;
(230 − 20 * 8) + (150 − 30 * 4) − кустов смородины и крыжовника осталось посадить;
20 * 8 − кустов смородины посадили садоводы;
20 * 8 + 30 * 4 − кустов смородины и крыжовника посадили садоводы;
230 − 20 * 8 − кустов смородины осталось посадить;
20 * 8 − 30 * 4 − на сколько кустов смородины посадили больше, чем крыжовника;
(230 − 20 * 8) − (150 − 30 * 4) − на сколько кустов крыжовника осталось посадить меньше, чем смородины;
30 * 4 − крыжовника посадили садоводы.
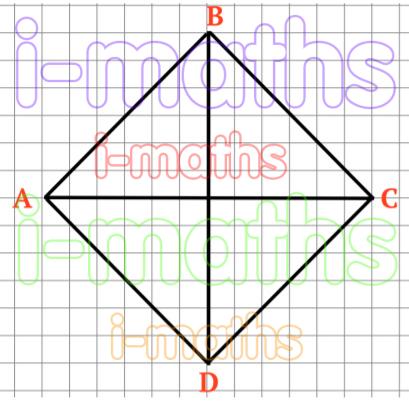
4. Начерти в тетради отрезки AC и BD, как показано на рисунке. Восстанови четырехугольник ABCD по его диагоналям AC и BD. Выполни измерения и вычисли периметр этого четырехугольника в
сантиметрах. Что можно сказать о длинах сторон этого четырехугольника? Является ли он квадратом?
Нет
Почему?
Углы не прямые
Можно ли изменить чертеж, чтобы четырехугольник ABCD стал квадратом?
Да
Объясни свой ответ.
1) Начертим четырехугольник по его диагоналям.
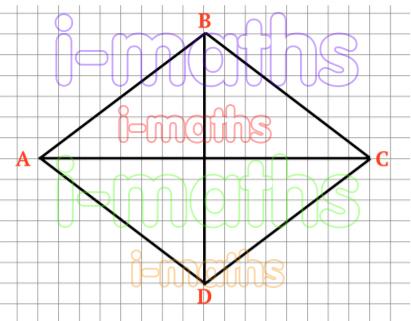
2) Найдем его стороны:
AB = BC = CD = AD = 5 (см)
3) Найдем периметр четырехугольника:
(5 + 5) * 2 = 10 * 2 = 20 (см)
4) Стороны этого четырехугольника равны.
5) Данный четырехугольника не является квадратом, так как полученные углы на прямые.
6) Чтобы получился квадрат нужно провести диагонали так, чтобы они были одинаковые:
AC = 8 см
ВD = 6 см
8 − 6 = 2 (см), значит можно уменьшить AC на 2 см или увеличить BD на 2 см, чтобы ABCD стал квадратом.