Вспомни, что означает каждое число в записи двух чисел со знаком умножения: 3 ∙ 4, 6 ∙ 3.
- 3 ∙ 4 = 3 + 3 + 3 + 3 = 12
3 – первый множитель, 4 – второй множитель, а 12 – произведение. Значит число 3 взяли 4 раза.
- 6 ∙ 3 = 6 + 6 + 6 = 18
6 – первый множитель, 3 – второй множитель, а 18 – произведение. Значит число 6 взяли 3 раза.
Номер 1
Рассмотри суммы и скажи, чем они похожи.
Суммы похожи тем, что слагаемые в каждом ряду одинаковые, а значит сложение можно заменить умножением.
- 2 ∙ 8 = 16
- 7 ∙ 6 = 42
- 25 ∙ 4 = 100
- 13 ∙ 3 = 39
Номер 2
- 4 + 4 + 4 < 4 ∙ 5
- 16 + 16 + 16 = 16 ∙ 3
- 8 + 8 + 8 > 8 ∙ 2
- 32 + 32 < 32 ∙ 3
- 9 + 9 + 9 = 9 ∙ 3
- 48 + 48 = 48 ∙ 2
Номер 3
Рассмотри чертежи и объясни, почему верны равенства.
4 ∙ 2 = 2 ∙ 4
6 ∙ 3 = 3 ∙ 6
8 ∙ 3 = 3 ∙ 8
От перемены мест множителей их произведение не меняется.
Рассматриваю чертеж 1 и рассуждаю так: 4 ∙ 2 = 2 ∙ 4
4 ∙ 2 – в строке 4 клетки, всего строк 2.
2 ∙ 4 – в столбце 2 клетки, всего столбцов 4.
Произведения одинаковые, так как находим количество клеточек одного и того же прямоугольника.
Рассматриваю чертеж 2 и рассуждаю так: 6 ∙ 3 = 3 ∙ 6
3 ∙ 6 – в строке 3 клетки, всего строк 6.
6 ∙ 3 – в столбце 6 клетки, всего столбцов 3.
Произведения одинаковые, так как находим количество клеточек одного и того же прямоугольника.
Рассматриваю чертеж 3 и рассуждаю так: 8 ∙ 3 = 3 ∙ 8
3 ∙ 8 – в строке 3 клетки, всего строк 8.
8 ∙ 3 – в столбце 8 клетки, всего столбцов 3.Произведения одинаковые, так как находим количество клеточек одного и того же прямоугольника.
Номер 4
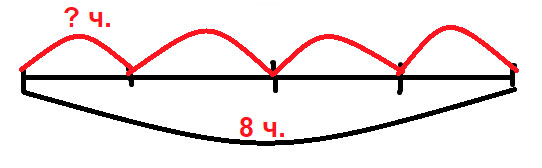
Составь по рисунку задачу на умножение и две обратные ей задачи.
Первую группу 3 «А» класса разделили на 4 пары. В каждой паре по 2 человека . Сколько всего человек в 1 подгруппе 3 «А» класса?
1) 2 ∙ 4 = 8 (ч.)
Ответ: 8 человек
Обратная задача №1: 1 подгруппу, в которой учится 8 ребят, разделили на 4 группы. Сколько человек в каждой группе?

1) 8 : 4 = 2 (ч.)
Ответ: 2 человека в каждой группе.
Обратная задача №2: 1 подгруппу, в которой учится 8 ребят, разделили на пары по 2 человека в каждой. Сколько пар получилось?
1) 8 : 2 = 4 (п.)
Ответ: 4 пары.
Номер 5
Легковое такси может взять 4 пассажиров. Сколько пассажиров могут взять 3 такие машины? Составь две задачи, обратные данной, и реши их.
1) 4 ∙ 3 = 12 (п.)
Ответ: 12 пассажиров.
Обратная задача №1: Легковое такси может взять 4 пассажиров. Сколько таких машин нужно для перевозки 12 пассажиров?
1) 12 : 4 = 3 (м.)
Ответ: нужно 3 машины.
Обратная задача №2: В 3 легковые машины такси разместилось 12 пассажиров. Сколько пассажиров было в каждой машине?
1) 12 : 3 = 4 (п.)
Ответ: в каждой машине по 4 пассажира.
Номер 6
Составь задачи по кратким записям и реши их.
Задача №1: У Ани было 50 рублей. Она купил пирожок за 14 рублей и сок за 6 рублей. Сколько денег осталось у Ани?
1) 14 + 6 = 20 (руб.) – потратила Аня на покупку
2) 50 − 20 = 30 (руб.) – осталось
Ответ: 30 рублей.
Задача №2: Папа дал дочери 30 рублей и мама дала ещё 15 рублей. Маша позавтракал в школе, после чего у него осталось 20 рублей. Сколько стоил завтрак в школе?
1) 30 + 15 = 45 (руб.) – было
2) 45 − 20 = 25 (руб.) – стоил завтрак
Ответ: 25 рублей.
Задание внизу страницы
Сколько лап у восьми цыплят?
2 ∙ 8 = 16 (л.)
Ответ: у 8 цыплят 16 лапок.
