Номер 2
Рассмотри чертёж. Назови диагонали квадрата и точку их пересечения. Что можно сказать о свойствах диагоналей квадрата, зная, что квадрат тоже прямоугольник? У диагоналей квадрата есть ещё одно свойство. При пересечении диагоналей квадрата получаются четыре прямых угла. Проверь это свойство по чертежу.

Номер 3
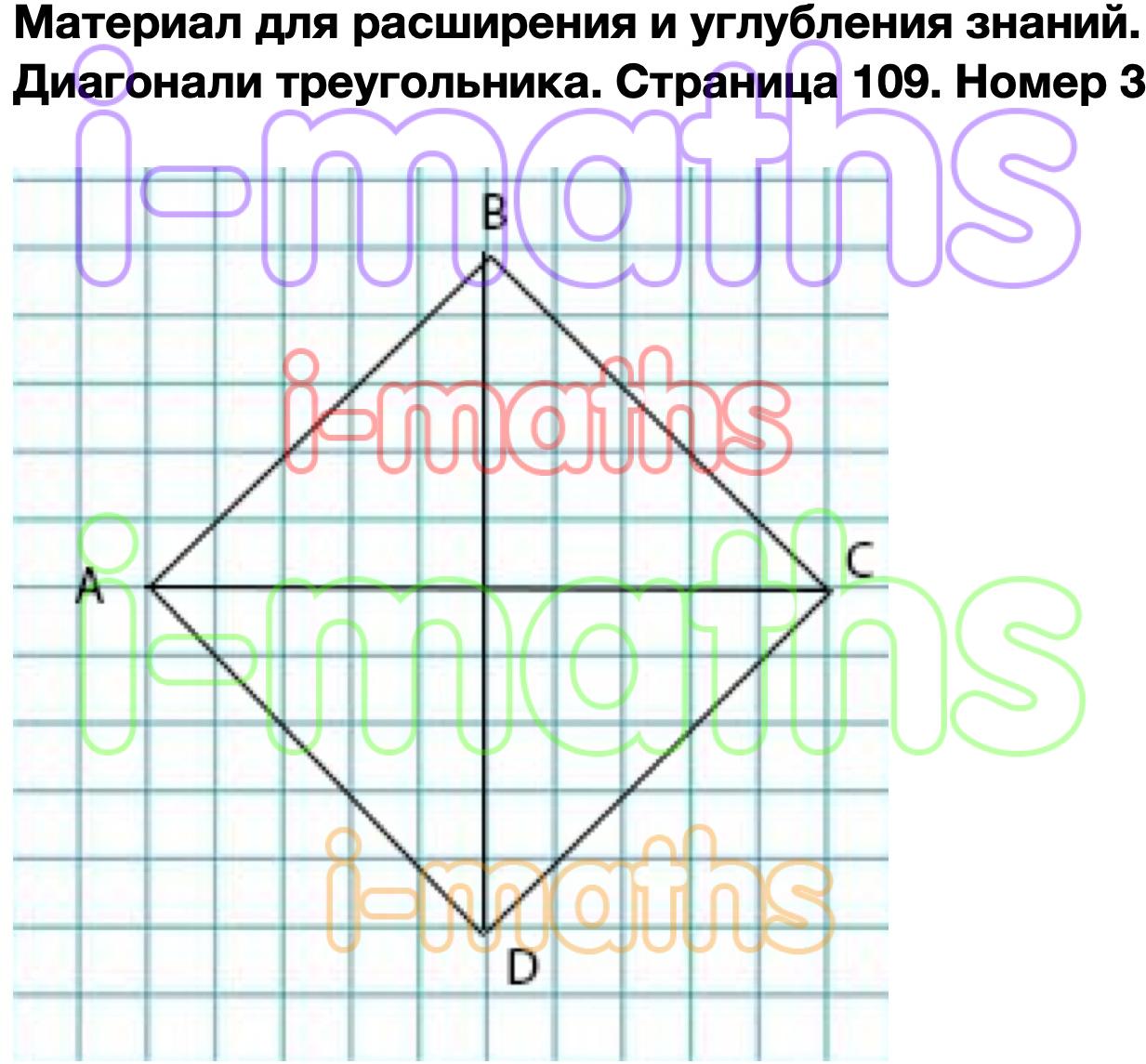
Используя свойства диагоналей квадрата, начерти в тетради квадрат, длина диагонали которого 5 см.
Номер 4
Построить 4 прямых угла с общей вершиной можно и на нелинованной бумаге.
1) Отложи на прямой отрезок АВ. Радиусом, равным больше половины длины отрезка, проведи 2 окружности с центрами в точках А и В (чертёж 1). Обозначь точки пересечения окружностей буквами С и D. Проведи прямую через точки С и D. Точку пересечения прямых обозначь буквой О. Проверь, что все 4 угла с вершиной в точке О прямые. Вместо окружностей можно проводить дуги (части окружностей) любого радиуса, который всегда должен быть больше половины длины отрезка АВ.
2) Построй 4 прямых угла с общей вершиной в точке О, следуя плану пункта 1, но вместе окружностей проводи дуги (чертёж 2). Любую точку отрезка CD соедини отрезками с точками А и В. Убедись, что полученный треугольник – равнобедренный. Начерти так же ещё 2 равнобедренных треугольника; 1 равносторонний.

